In Part I of this series, I presented the reasons I'm interested in optimisation, and gave a mathematical statement of the example constrained optimisation problem I will solve. In this post, I am going to present two practical implementation algorithms, coded in R. I'll also present an R function for visualising the resultant circles.

Code for optimisation and visualisation can be found at the end of this post. It's fairly well commented, so just some general comments first:

Most optimisation functions take a single vector of parameter values as an argument. This is a bit unwieldy for our problem, since we have N triplets of x,y and $r$. Here I arbitrarily define a parameter vector z, of length 3N and split it up (consistently) into vectors for x, y and r.

R has a convenient combinatorics facility, so I use that to generate a unique list of all possible circle pairs to optimise the calculations required for constraint $g_5$.

I'm using function closures here to avoid defining global variables. In R, a function closure is a function which returns another function, together with its own environment for storing variables etc., which can be initialised within the outer function before returning the inner function. For example, I have created a function createObj which initialises the number of circles N, and the rectangle dimensions (W and H), generates a unique list of circle pairs (cpairs) and creates a function newObj which only depends on z, but nevertheless has access to private copies of N, W, H and clist.

Here, constraints are embedded into the objective function. A numerical value quantifying constraint violation is subtracted from the objective function we are trying to maximise. There are two alternative versions of the objective function closures in the code below: createObj is "soft", the constraint violation values are the sum of the square of the magnitude of violations, createHardObj is "hard", any single violated constraint, no matter how small, returns in an area of -Infinity. In the first case, a derivative based algorithm will always be able to figure out a path towards satisfying constraints if it finds itself in a region where they are violated, but small violations may be tolerated in the final solution. In the latter case, all constraints must be completely obeyed and so any solution will be perfect, but on the other hand, there are no hints about how to improve from an invalid set of parameters, and so finding a solution is much more difficult.

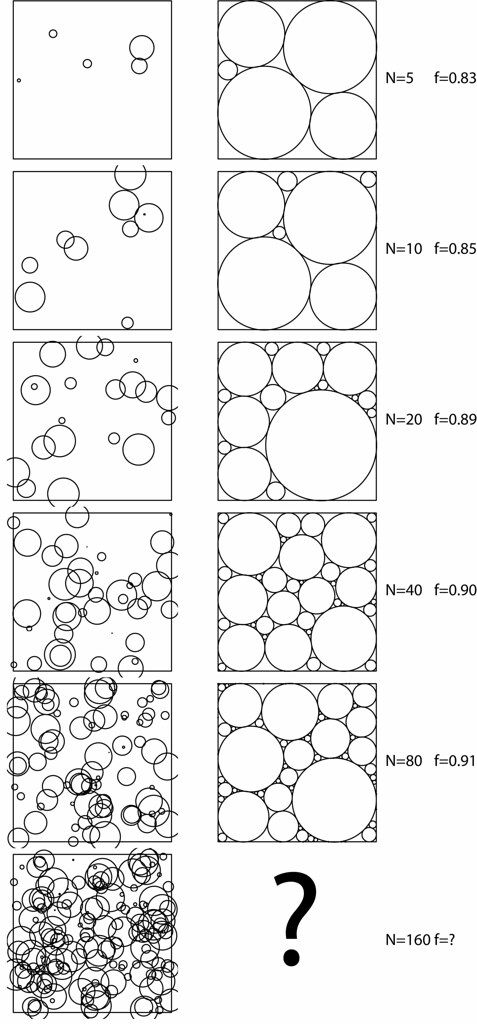
The drawCircles function can plot circles to screen, or in vector graphics format (to a .pdf for example). Here are some outputs generated with this function (initial guess on left, optimised result on right):

Finally, the optimisation routine presented here just uses the L-BFGS-B method which is a pretty good, bounded, derivative-based optimiser, which is made available within the optim function which is standard in R installations (it's part of the core). It's fairly slow for more than 100 circles, and the results are not perfect, as circles are often forced to the edge of the box with negligble radii. Nevertheless, it's a good start.