Rasterizing Archimedes Spirals

Imagine you want a list of coordinates, following a spiral, on a discrete, regular grid. I can think of several examples where this could be useful for digital image construction, where the regular grid corresponds to pixel coordinates (integer only). It's easy to code up a square spiral like Ulam's spiral, since pixels are naturally arrayed on a rectangular grid, but using square spirals in image construction leaves obvious square corners. A circular spiral can be smoother and better.

Let's look at the Archimedes spiral in polar coordinates:

$r(\theta)=a+b\theta$

If we choose a = 0 and select b so that:

$r(2\pi)-r(0)=\alpha$

we can write the equations describing the spiral in Cartesian coordinates, in terms of $\inline \alpha$ , the distance between spiral loops:

$x(\theta)=\frac{\alpha\theta}{2\pi}\cos(\theta)$

$y(\theta)=\frac{\alpha\theta}{2\pi}\sin(\theta)$

To get an approximation of this smooth curve on a regular grid, we can think about trying to move along it in jumps of constant length $\inline \omega$ , where the jump size is achieved by selecting a change in angle $\inline \delta$ . Computing the distance between one point and the next we can write down this expression:

$\80dpi \inline \omega={\sqrt{{\left( \frac{-\left( \alpha \,\theta \,\cos (\theta ) \right) }{2\,\pi } + \frac{\alpha \,\left( \delta + \theta \right) \,\cos (\delta + \theta )}{2\,\pi } \right) }^2 +{\left( \frac{-\left( \alpha \,\theta \,\sin (\theta ) \right) }{2\,\pi } + \frac{\alpha \,\left( \delta + \theta \right) \,\sin (\delta + \theta )}{2\,\pi } \right) }^2}}$

We can rearrange this expression into something simpler:

$\omega=\frac{{\sqrt{{\alpha }^2\,\left( {\delta }^2 + 2\,\delta \,\theta + 2\,{\theta }^2 - 2\,\theta \,\left( \delta + \theta \right) \,\cos (\delta ) \right) }}}{2\,\pi }$

It would be nice to solve this for $\inline \delta$ , then we would know how big an angle we need to jump to move exactly $\inline \omega$ at a given time. Remember that as the radius gets bigger, the angle required to achieve a given displacement decreases. Unfortunately, I can't solve it analytically, due to the presence of the cosine term, however we can approximate cos( $\inline \theta$ ) with the Taylor Series expansion up to 3rd order, giving us this expression:

$\omega=\frac{{\sqrt{{\alpha}^2\,\left(1+{\theta}^2\right)}}\,\delta}{2\,\pi}+{O(\delta)}^2$

This can easily be solved for small values of $\inline \delta$ . If we define the perpendicular distance between pixel centres as 1, we know that the maximum distance between any two adjacent pixels is 1/ $\inline \sqrt{2}$ . Therefore if we choose our parameters like this:

$\omega=\alpha=\frac{1}{\sqrt{2}}$

we would expect to move along the spiral, moving close to every pixel at least once. If we continue to step along the spiral like this indefinitely, and round every coordinate to the nearest integer value, we should hit every pixel in Archimedes spiral order!

This diagram shows the result of applying this algorithm:

The blue curve is a continuous Archimedes spiral, the numbered red points are the pixel approximations of the continuous curve and the red lines demonstrate the actual path taken between unique, discrete approximation points.

Below is a demonstration of what this sort of thing can look like. In this case I sorted the pixels of an original image by intensity and re-drew them along the approximate pixellated Archimedes spiral path:

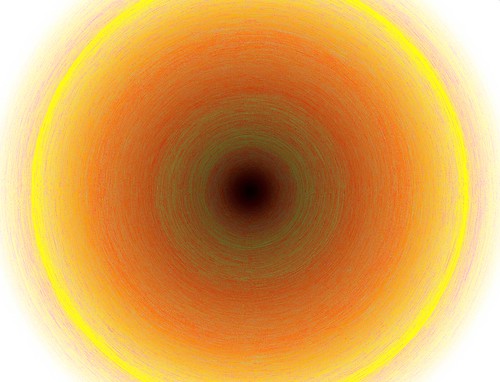
The original image is here:

I've written some python code to generate these rasterized pixel spirals. You specify an image size (rectangle) and the coordinates of the spiral focus, and it generates a unique list of points lying inside that rectangle, in spiral order (as in the diagram above). It's quite fast, it can generate enough points to fill a 6 megapixel image in a couple of minutes.

from math import *

 

def uniquer(seq, idfun=None): # http://code.activestate.com/recipes/52560/

    # Generates a unique list of elements from seq

    # maintaining their original order

    if idfun is None:

        def idfun(x): return x

    seen = {}

    result = []

    for item in seq:

        marker = idfun(item)

        if marker in seen: continue

        seen[marker] = 1

        result.append(item)

    return result

 

def x(theta,alpha):

    return int(round(alpha*theta*cos(theta)/(2*pi)))

 

def y(theta,alpha):

    return int(round(alpha*theta*sin(theta)/(2*pi)))

 

def delta(alpha, theta, omega):

    return (2*pi*omega)/sqrt(pow(alpha,2)*(1+pow(theta,2)))

 

def dist(a,b):

    return sqrt(pow(a[0]-b[0],2)+pow(a[1]-b[1],2))

 

def rasterspiral(TL,BR,F):

    # Distance between spiral loops

    alphas=1/sqrt(2)

    # Distance along spiral at each step

    omegas=1/sqrt(2)

    # Starting theta

    thetas=0

 

    # Define top left pixel and bottom right pixel coordinates

    (tlx,tly)=TL

    (brx,bry)=BR

    # Spiral focus coordinates (must lie within rectangle above)

    (xf,yf)=F

 

    # Find which corner is farthest from the spiral focus

    corners=[[tlx,tly],[tlx,bry],[brx,bry],[brx,tlx]]

    distances=[dist([xf,yf],i) for i in corners]

    farthestind=max(xrange(len(distances)), key=distances.__getitem__)

    farthest=corners[farthestind]

 

    # Initialise the spiral at F

    xc,yc=xf,yf

    results=[(xc,yc)]

 

    # Keep spiralling until we've capture the farthest corner

    while [xc,yc]!=farthest:

        # Update the step in angle based on current angle etc.

        deltanew=delta(alphas,thetas,omegas)

        thetas=thetas+deltanew

        # Calculate the next coordinates

        xc,yc=xf+x(thetas,alphas),yf+y(thetas,alphas)

        # If these coordinates lie within the defined rectangle

        # then store them

        if tlx<=xc<=brx and tly<=yc<=bry:

            results.append((xc,yc))

 

    # Now eliminate duplicate copies of points on the spiral

    results=uniquer(results)

    return results

 

# Example of use:

test=rasterspiral((0,0),(50,100),(25,50))

Conor Lawless

Scientific Computing

http://cnr.lwlss.net

Rasterizing Archimedes Spirals